バスレフ型スピーカーは、スピーカーユニットの背後から出る音を利用して低音を増強しようとする方法です。
背後から出る音を、反転させて前面に押し出すようになることから、位相反転型スピーカーともいいますが、一般的には低音を反転されるという意味でしょう、バス・レフレックス方式と名づけられ略してバスレフ型と言われています。
(鏡の反射を利用して高倍率としたカメラ用レンズも、レフレックスレンズと呼ばれますね)
密閉型スピーカーは、スピーカー背後は閉じられた空気室となっていますが、この空気室に穴を開けるとバスレフ型となります。
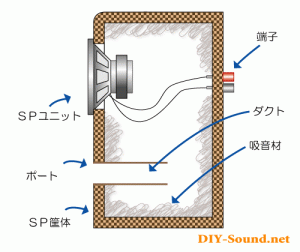
 開放された穴をポート、ポートから後ろに続くパイプ部分をダクトといいます。本を読んでいると、板に穴を開けただけでも板の厚みがパイプ状態になるので、その部分がダクトとして機能すると書いてあります。
開放された穴をポート、ポートから後ろに続くパイプ部分をダクトといいます。本を読んでいると、板に穴を開けただけでも板の厚みがパイプ状態になるので、その部分がダクトとして機能すると書いてあります。
 バスレフ型にすると、空気室の容量とダクトの長さにより共振周波数が発生します。これをうまく調整することで低音強調がなされたスピーカー特性となることから、比較的容易に低音を引き出す方法として市販品でも圧倒的にバスレフ型が多いところです。
バスレフ型にすると、空気室の容量とダクトの長さにより共振周波数が発生します。これをうまく調整することで低音強調がなされたスピーカー特性となることから、比較的容易に低音を引き出す方法として市販品でも圧倒的にバスレフ型が多いところです。
ポートの形状は円である必要はなく、四角形や細い長方形でも大丈夫です。形状による特性の違いは多少あるでしょうが、共振周波数としては断面積が影響するところです。
 このダクトの共振は、ヘルムホルツの法則により導かれます。
このダクトの共振は、ヘルムホルツの法則により導かれます。
法則ですから、何やら難しい式が存在しておりますがここでは割愛^^
要は、「空気室の容量と、ダクトの長さと断面積で、共振する周波数が決まりますよ~」というものです。
計算式は難しいので、いつか数値を入れると計算できるツールを置きたいものです^^(追記:下記に共振計算の参考ページ設置)
例えば、上のイラストのようなスピーカーを想定して、
・高さ40cm ・幅20cm ・奥行き30cm
・ダクトの長さ 20cm ・ダクト断面積 30c㎡(15cm×2cm)
としますと、このときの共振周波数は約40Hzとなります(板の厚みは考慮してません)。
仮にダクトの長さが10cmだとしたら、共振周波数は約50Hzとなります。
ダクトの断面積を半分にして、共振周波数を約40Hzにしようとすれば、ダクトの長さは約8.5cmで済む計算になります。
ただ、あまりダクトを細くしたり、長くしたりすると低音域の量感が足りなくなる可能性がありますので、そこはユニットとの関係も含めて適正なところを探ることになります。
実際にはスピーカーユニットの振動板面積やスピーカーの持つ特性(抵抗)も左右してきますから、上記のように法則より導かれる数値になるかというとなかなかそうでもないところ(汗)。
ま、なので自作の面白いところでもあります。計算通りにいかないかと思えば、逆に思わない効果が出てきたりと^^
さて、でもなんだかバスレフの効果って分かりにくいですね。
そこで、よく次のように例えられます。
・スピーカー → ピストン
・空気室 → バネ
・ダクト → 重り
空気室は、密閉型であればスピーカーの振動により揺さぶられても、空気の出入りする場所がありません。なので、振動板が裏側へ動けば圧縮された空気が振動板を押し返すバネ効果を生みます。
バスレフ型もダクトにより外部と空気の移動があるにしても、それは平面バッフルや後面開放型とは比べられない抵抗が生じていますので、密閉型に及ばないまでもバネ効果が生じているといえます。
ダクトは、長さと太さで抵抗が変化します。
太くて短いダクトより、細くて長いダクトの方が当然ながら空気の移動が妨げられます。これが重りの大小と置きかえられます。
それを考えてイラストにすると次のようになります。
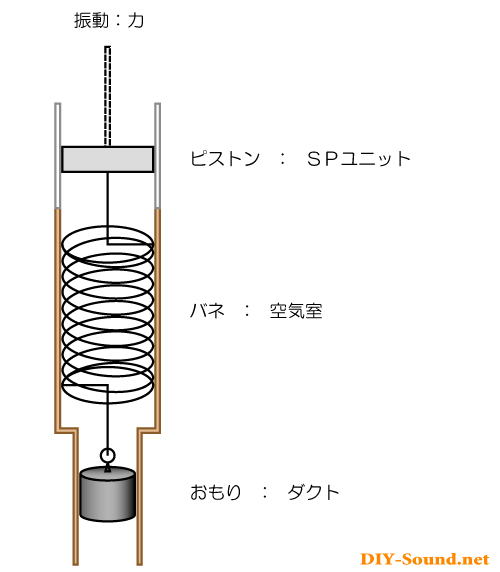 そこで想像してみてください。
そこで想像してみてください。
例えばバネでなくても輪ゴムでもイメージできると思うのですが、輪ゴム(バネ)におもりを結んでぶら下げます。
手を上下に動かすと当然おもりも上下に動きます。
そしてタイミングよく、輪ゴム(バネ)に適度なテンションがかかるように上下運動すると、輪ゴム(バネ)の力を利用して効率よく上下できるポイントがあると思います。
なかなか手の動きはタイミングを統一することができないので再現が難しいですが、手の運動は輪ゴム(バネ)が伸びきる前に引き上げる動作をし、縮みきる前に今度は下げる動作に入るようになります(輪ゴム(バネ)の場合には縮むことへの反発がほぼありませんが、スピーカーの空気室では圧縮された空気が反発します)。それにより輪ゴム(バネ)の反発力(?)を効率的に使って上下運動させていることになります。
つまり、おもりの動きは輪ゴム(バネ)反発力を利用することで手の動きとは逆になる、手の動きの速さの範囲があるといえますよね。
これを分かりやすいように、アニメーションを作ってみました。
(やや強引ですがこんな感じではないでしょうか^^)
※表示画面でアニメーションが動かない場合は、画像をクリックしてみてください。
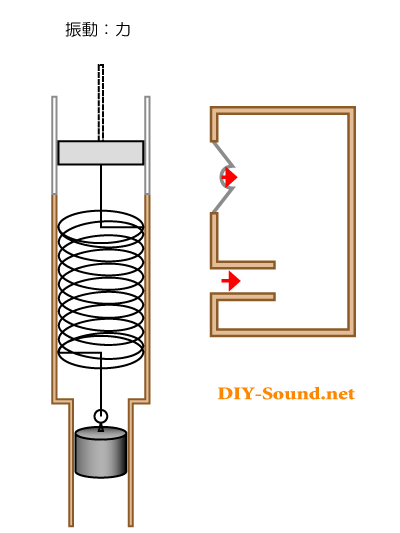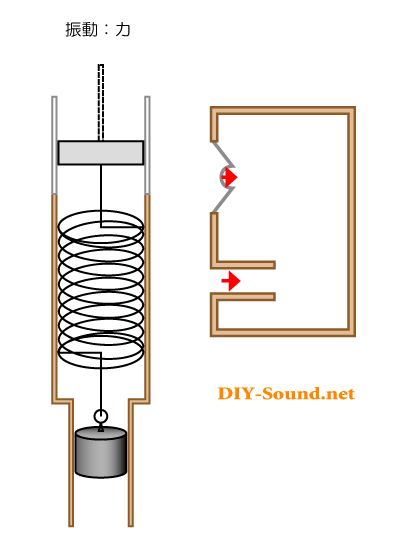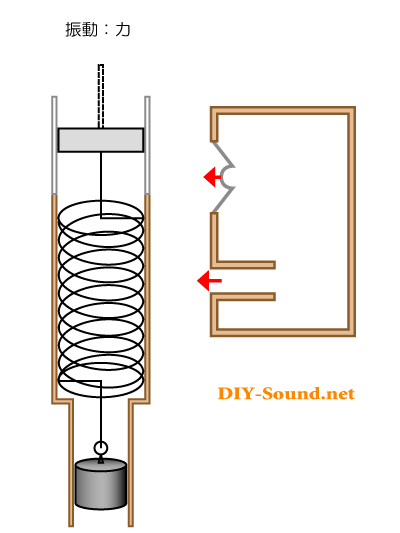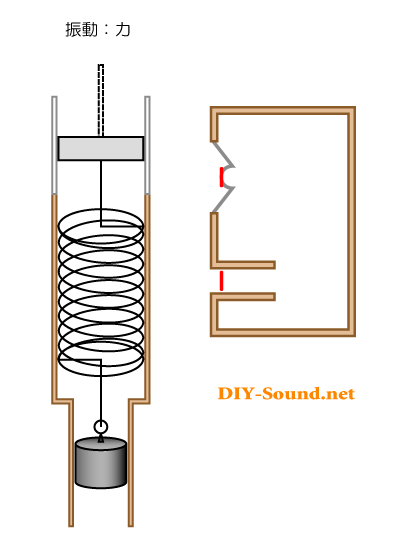
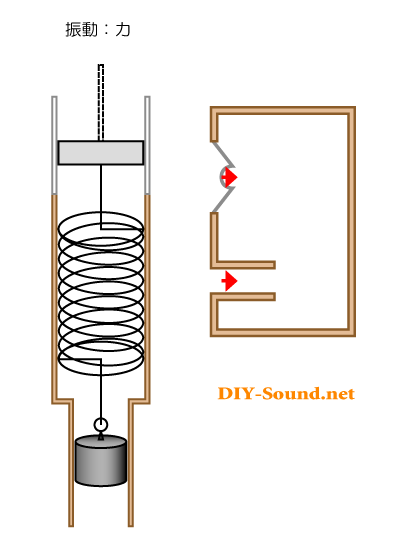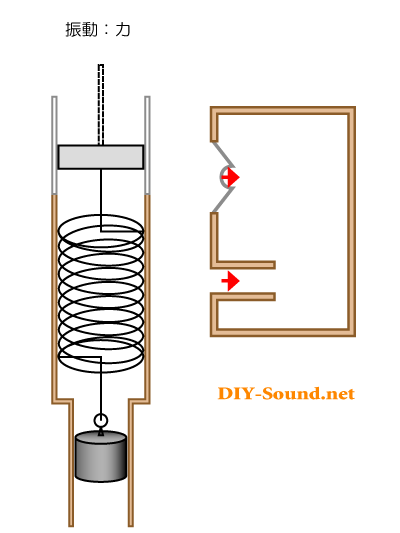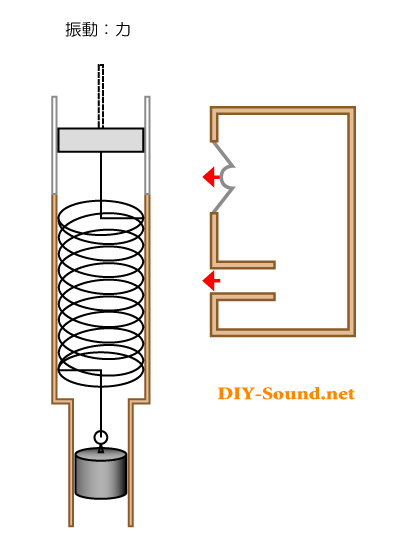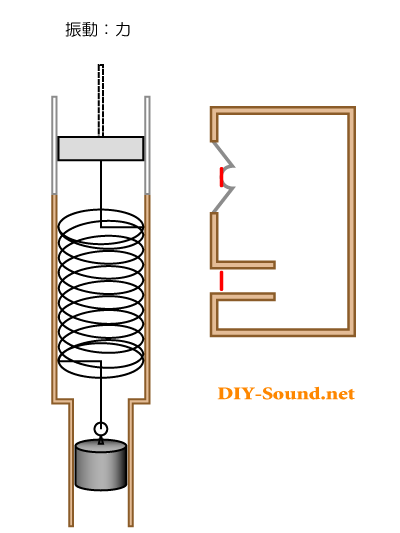 ピストン=バネ=おもり の動くイメージにあわせて、バスレフ型スピーカーの動きも入れてみました。
ピストン=バネ=おもり の動くイメージにあわせて、バスレフ型スピーカーの動きも入れてみました。
ご覧のように、矢印の向きが同じになります。
つまりは、スピーカーの裏側の音を前面に押し出す
ということで、これが位相反転型スピーカーとか、バス・レフレックス型スピーカーといわれる原理です^^
この動きは、バスレフ型スピーカーの最低共振周波数より高い音域ではこういった動作作用が働いています。
さらに、上のアニメーションはピストンとおもりの上下の振幅長は同じになってますが、共振のバネ効果が効いてくるとピストンよりおもりの上下振幅長が大きくなる“はず”です^^
それをアニメーションにしてみると、
※表示画面でアニメーションが動かない場合は、画像をクリックしてみてください。
バネの力を最大に活用するのは、最も振幅が大きくなるポイントです。そのポイントでこの効果が最大になりますよね。
それがバスレフ型スピーカーエンクロージャの最低共振周波数ということになります。
このポイントを超えると力関係の均衡が崩れてしまい、ピストンとおもりの連動する動きが崩れてしまう、ということになります。
さて、この位相反転させる音ですが、音の速さの中の僅かなタイミングながら、スピーカーより出された音はワンクッション置いてダクトより出ていることになります。
ユニット正面の音よりほんの少し遅れている音、ということになりますね。
なので、低音は気にならないところですが、中高音域はできるだけ漏れないようにした方が良いわけで、そこで吸音材がいろいろと工夫されてもいるところです。
でも、吸音材も入れすぎると元気のない音になるし、低音の量感まで奪うときがありますから、なるべくスピーカー形状で高音域をカットできる方が望ましいかなと、個人的には思います(空気室の大きさやダクト形状など)。
さて再び輪ゴム(バネ)とおもりを想像してください。
輪ゴム(バネ)のテンションをうまく利用しながらの上下作業、でもその手の動きをどんどん遅くしたらどうなるでしょうか?
先述のように、ピストンとおもりの力の均衡が崩れてしまった場合の想定です。
あるスピードを下回ると、輪ゴム(バネ)は反発することなく、手の上下の動きにそのまま追従するようになるはずです。
こんな感じに…
※表示画面でアニメーションが動かない場合は、画像をクリックしてみてください。
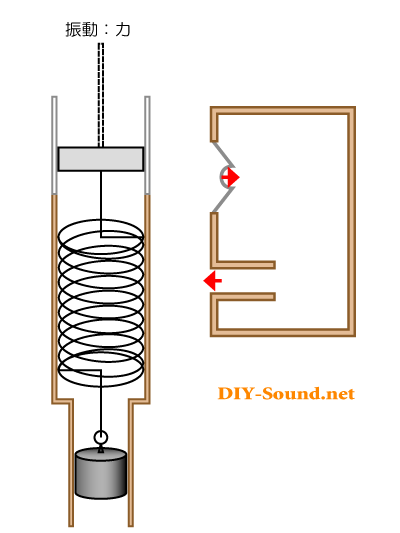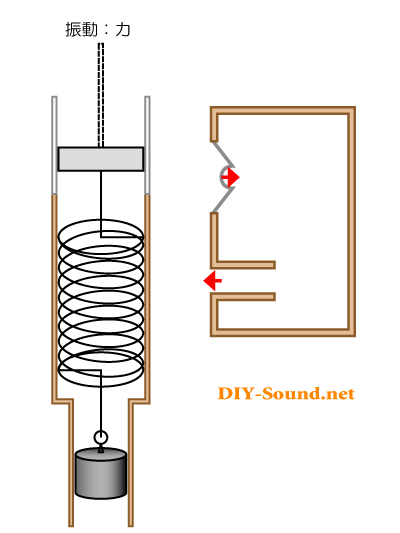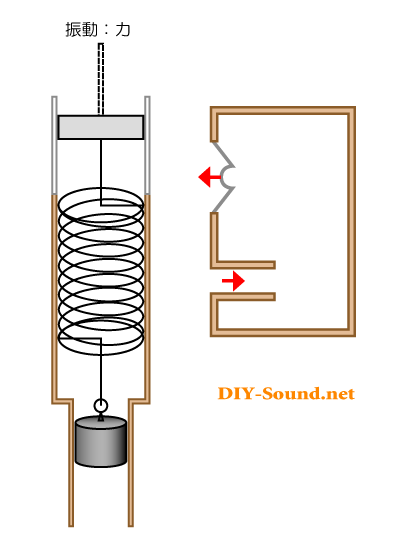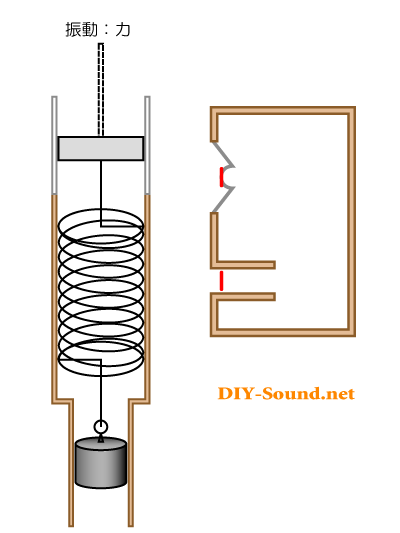 今度は、矢印の動きは逆向きになりました。
今度は、矢印の動きは逆向きになりました。
バスレフ型としての、反転させる効果は失われておりますね。
これが最低共振周波数を下回った周波数での動作となります。
単純ではないでしょうが、これはスピーカー前面の音を打ち消すような動きでありまして、実際バスレフ型スピーカーの最低共振周波数から下の低音域の量感は急速に低下します。
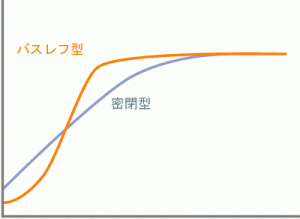
特性としては、密閉型がなだらかに下がりながらも低音域を伸ばすのに対して、バスレフ型は最低共振周波数まで量感を保ちつつ、それ以降はストンと落ちる、そんな特性傾向となります。
市販製品のほとんどがバスレフ型です(その亜種のような存在もたくさん^^)
スピーカー背面の音をいかに有効利用して、その効果を得ることができるか、手作りスピーカーとしても楽しめる部分と思います。
なので、このバスレフ型とバックロード型に自作派が挑むことが多いですよね~
スピーカーの自作、手作りの音は面白い^^
(※)追記
細かい法則等には触れず(よ~分かりません)、なるべく分かりやすいようにご説明している“つもり”であります^^。
自分もバスレフの原理がよく分からずにいましたので、このページを作成しながらいろいろ調べました。
上の説明やイラストで全てが説明できるものでもないでしょうが、バスレフ型の動作イメージとしては参考になると思います。
(誤りがなければよいのですが…大汗)
その他いろいろと初心者向けに分かりやすい情報がありましたらお待ちしております。
2008年03月08日作成
2008年03月15日加筆
2008年03月19日修正・加筆
2017年02月07日加筆
2017年08月13日誤字修正
コメント & トラックバック